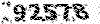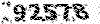y`(x)=(G.M/R^2.c^2)x
y`(2R)=2G.M/R.c^2
شعاع شوارتزشلید <------R0=2G.M/c^2
D=R0/R
انحرافی را که به دست آوردیم،دقیقا با مقدار انحرافی که بر مبنای مکانیک نیوتونی بدون تقریب به دست می آید برابر است.
ولی بر پایه و بنیاد نسبیت عام مقدار به دست آمده دقیقا 2 برابر مقدار بالا است.
شاید اگر زمانی که از اینشتین می پرسیدند"اگر رصد خورشیدگرفتگی در آفریقا نظریات او را رد می کرد،اینشتین چه می کرد؟" و او نمی گفت که "به آزمایش کننده شک می کردم" این چنین طبیعت او را یاری نمی کرد که درست 2 برابر چیزی که نیوتون می گوید جوابِ درست باشد!
اینشتین یک طرف خط بود و شادمان از اینکه به سوالی که در ذهن داشته پاسخ داده است.و کسانی چون سلندر آن طرف خط بودند و سعی داشتند رفتار نور را بررسی کنند و ببینند این موج در ارتباط با ماده و دستگاه های مختلف چه خصوصیاتی از خود نشان می دهد.
اصلا شاید ذره نباشد!!!!
شانس به کسی روی می آورد که به شانس اعتقادی نداشته باشد!
اینشتین شانس آورد که این طرف خط بود ،نه فیزیکدان خبره ای بود، نه ریاضی دان کهنه کاری. او فقط می خواست به سوالات ساده ای که در ذهنش پیش می آید پاسخ دهد.
ابتدا شاید قصد جسارت و دخالت در محاسبات سنگین الکترومغناطیسی و گرانشی را نداشت. ولی پاسخ سوالش او را به یک حالت مرزی و حدی برد.
فایده ی حالات مرزی را می توان با این مثال مشخص کرد که کسی که در مرز مسئله ای قرار بگیرد، می تواند مسئله را درحالت کلی تری ببیند،که حالت خاص درون مسئله ی اولی را هم شامل می شود. ولی کسی که نمی تواند مرز مسئله را ببیند گمان می کند که کل، یعنی مسئله ی او. و جوابی را هم که پیدا می کند، حالتی عمومی می پندارد.
اینشتین یک شانس دیگر هم آورد، اینکه شهرتی در علم نداشت،همین باعث شد که جسارت پیدا کند.
این که سرعتی بیش از سرعت نور وجود نداشته باشد به نظر شوخی بزرگی می آمد ، ولی کوچکتر ها حق شوخی کردن دارند! اما اینشتین حتی نمی خواست شوخی کند . او فقط می خواست جواب سوالش را بدهد.
کم کم با همکاری همسرش، این اصولی را که برای دنیای خودش ساخته بود، به معادلات کشانید و نتایجی به دست آورد که در دنیای همه ی ما صادق است،بزرگترها کم کم قبول کردند که اصول دنیای اینشتین در دنیای آنها هم حکمرانی می کند.
دربخش بعد با چند مثال شما را در لذت نتایجی که اینشتین به خاطر پاسخ به یک سوال ساده به دست آورد شریک خواهم کرد.